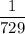Answer:
The probability of advancing to the seventh round is:
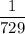
Explanation:
It is given that:
In each round of a game show, a contestant answers a multiple-choice question that has three answer choices.
Also, the contestant advances to the next round by answering the question correctly.
Hence, in order to reach the seventh round he has to correctly answer in all of the preceding rounds (i.e. round 1 to round 6)
Now, as we know that the event of answering in each round is independent of the other rounds.
Hence, the probability of advancing to the seventh round is product of probability of answering correctly in all the preceding rounds.
Let P denotes the probability of an event.
P( answering round 1 correctly)=P(1)=1/3
( since, we know that out of three choices only one is correct)
P( answering round 2 correctly)=P(2)=1/3
Similarly,
P( answering round 3 correctly)=P(3)=1/3
P( answering round 4 correctly)=P(4)=1/3
P( answering round 5 correctly)=P(5)=1/3
P( answering round 6 correctly)=P(6)=1/3
Hence,

Hence, the probability is: