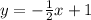Answer:
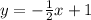
Explanation:
The equation of a line is
 where m is the pending and b is the y intercept,
where m is the pending and b is the y intercept,
First we are going to calculate m:
If you have two points
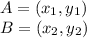 ,
,

Now we have, A=(-6,4) and B=(-2,2),
 replacing in the formula:
replacing in the formula:
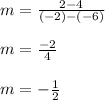
Then
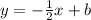
We have to find b, we can find it replacing either of the points in
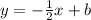
Replacing with (-2,2),
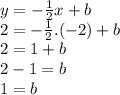
or replacing with (-6,4)

You can see that the result is the same, then the equation of the line is: