Question

What equation can be used to find the length of AC

(10)sin(40°)=AC
(10)cos(40°)=AC
10/sin(40°)=AC
10/cos (40°)=AC

Answer 1

(10)sin(40°)=Ac

Explanation:

Answer 2

ANSWER


`(10)sin(40 \degree) = AC`


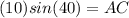
EXPLANATION

The given triangle ABC is a right angle triangle.

Side AC of ∆ABC is opposite to the known angle which is

`40 \degree`

The hypotenuse of the right angle triangle ABC is 10 in.




We use the sine ratio to arrive at the required equation.


Recall that, the sine ratio is given by

`\sin( \theta) = (length \: of \: opposite \: side)/(length \: of \: the \: hypotenuse)`



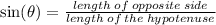
This implies that,



`\sin(40 \degree) = (AC)/(10)`


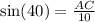
We now make AC the subject to obtain,



`AC = (10) \sin(40 \degree)`



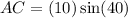
The correct answer is A.