Question

True or false? to find the area of a sector, you multiply the area of the circle by the fraction of the circle covered by that sector.

a.true

Answer 1

ITs true

Explanation:

just did the test

Answer 2

True

Explanation:

The area of a sector can be found in two ways:

First. With a formula in degrees.

`A=(\pi r^2 \alpha^(\circ))/(360^(\circ))`

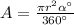
Second. With a formula in radians.

`A=(r^2 \beta )/(2)`

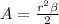
For example, for a sector α = 180° (β = π). we have:

`A=(\pi r^2 \alpha^(\circ))/(360^(\circ)) \therefore A=\frac{\pi r^2 180^(\circ)} {360^(\circ)} \therefore A=(\pi r^2)/(2)\\ \\ \\ A=(r^2 \beta )/(2) \therefore A=(r^2 \pi )/(2) \therefore A=(\pi r^2)/(2)`

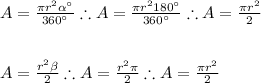
As you can see, from the two forms we have found out that if you want to find the area of a sector, you multiply the area of the circle by the fraction of the circle covered by that sector, because 180° (π) represents half a circle.