Question

Daisy walks across a force platform and the forces exerted by her foot during a step are recorded. The peak vertical reaction force is 1200 N (this force acts upward on Daisy). At the same instant, the braking frictional force is 200 N (this force acts backward on Daisy). How large is the resultant of these two forces? What is the direction of the resultant force?

Answer 1

The direction of the resultant force is approximately 189.462º.

The magnitude of the resultant force is approximately 1216.553 newtons.

Step-by-step explanation:

Let consider postive the direction of motion of Daisy's foot and the upward direction (perpendicular to direction of motion). Friction (
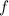`f`), measured in newtons, is directed against motion, whereas normal force from ground to the foot (
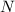`N`), measured in newtons, is in the upward direction. Then, resulting direction must be greater than 180º but less than 270º with respect to the axis of the direction of motion, which is found by the following formula:

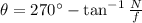`\theta = 270^(\circ)-\tan^(-1) (N)/(f)` (1)

Where
`\theta` is the direction of the resultant force, measured in sexagesimal degrees.

If we know that
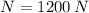`N = 1200\,N` and
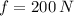`f = 200\,N`, then the direction of the resultant force is:

`\theta = 270^(\circ)-\tan^(-1) (1200\,N)/(200\,N)`

`\theta \approx 189.462^(\circ)`

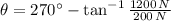
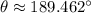
The direction of the resultant force is approximately 189.462º.

The magnitude of the resultant force (
`F`), measured in newtons, is determined by Pythagorean Theorem:

`F = \sqrt{f^(2)+N^(2)}`

`F =\sqrt{(200\,N)^(2)+(1200\,N)^(2)}`

`F \approx 1216.553\,N`

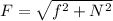
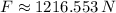
The magnitude of the resultant force is approximately 1216.553 newtons.