Question

Water flows from the bottom of a storage tank at a rate of r(t) = 200 − 4t liters per minute, where 0 ≤ t ≤ 50. find the amount of water that flows from the tank during the first 35 minutes.

Answer 1

The amount of water that flows from the tank during the first 35 minutes is 4550 liters.

Explanation:

We know that the rate is given by
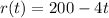`r(t)=200-4t` and the problem asks for the net change (the amount of water) for the first 35 minutes.

We can use the Net change theorem:

The integral of a rate of change is the net change:

`\int\limits^b_a {F'(x)} \, dx =F(b)-F(a)`

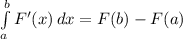
Applying the above theorem we get

`\int\limits^(35)_0 {200-4t} \, dt`

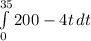
`\int _0^(35)200dt-\int _0^(35)4tdt\\\\\left[200t\right]^(35)_0-\left[(t^2)/(2)\right]^(35)_0\\\\7000-2450\\\\4550`

The amount of water that flows from the tank during the first 35 minutes is 4550 liters.