The distance between the two stations is 37.08 km

Step-by-step explanation:
Given:
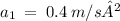
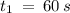
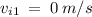
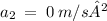
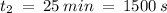
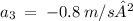
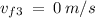

Required:
Distance from Station A to Station B

Equation:
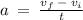
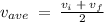
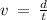

Solution:
Distance when a = 0.4 m/s²
Solve for
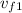
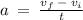
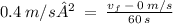
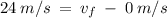
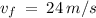

Solve for
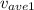
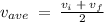
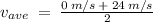
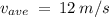

Solve for
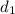
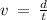
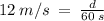
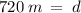
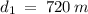

Distance when a = 0 m/s²
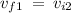
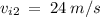

Solve for
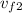
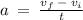
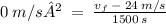
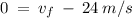
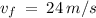

Solve for
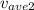
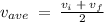
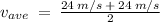
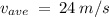

Solve for
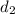
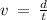
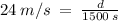
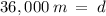
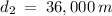

Distance when a = -0.8 m/s²
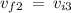
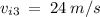

Solve for
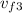
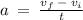
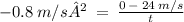
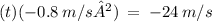
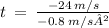
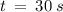

Solve for
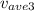
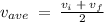
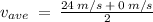
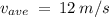

Solve for
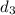
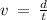
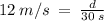
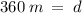
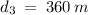

Total Distance from Station A to Station B
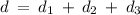
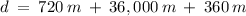
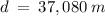
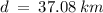

Final Answer:
The distance between the two stations is 37.08 km