For the work-energy theorem, the work done to accelerate the proton is equal to the variation of kinetic energy of the proton:

where
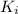
is the initial kinetic energy, which is zero because initially the proton is at rest.
We need to find the kinetic energy of the proton: we can't use the classical formula
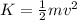
since the proton is at relativistic speed. Therefore, we must use the relativistic formula:
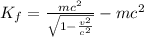
where
m is the proton mass
v is its final speed
c is the speed of light
Substituting
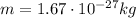
, v=0.987 c and

, we find
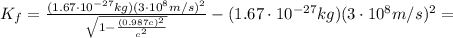
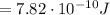
and this is equal to the work needed to accelerate the proton up to a speed of 0.987c.