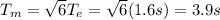Question

On earth, you swing a simple pendulum in simple harmonic motion with a period of 1.6 seconds. what is the period of this same pendulum on the moon? assume the moon's acceleration due to gravity is 1/6 of the acceleration due to gravity on earth.

Answer 1

The period of a simple pendulum is given by

`T= 2 \pi \sqrt{ (L)/(g) }`
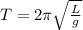
where
L is the pendulum length
g is the acceleration of gravity

If we move the same pendulum from Earth to the Moon, its length L remains the same, while the acceleration of gravity g changes. So we can write the period of the pendulum on Earth as:

`T_e= 2 \pi \sqrt{ (L)/(g_e) }`
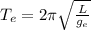
where
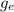
`g_e` is the acceleration of gravity on Earth, while the period of the pendulum on the Moon is

`T_m= 2 \pi \sqrt{ (L)/(g_m) }`
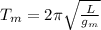
where
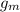
`g_m` is the acceleration of gravity on the Moon.

If we do the ratio of the two periods, we get

`(T_m)/(T_e) = \sqrt{ (g_e)/(g_m) }`
but the gravity acceleration on the Moon is 1/6 of the gravity acceleration on Earth, so we can write
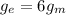
`g_e = 6 g_m` and we can rewrite the previous ratio as

`(T_m)/(T_e) = \sqrt{ (6 g_m)/(g_m) }= √(6)`

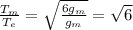
so the period of the pendulum on the Moon is

`T_m = √(6) T_e = √(6) (1.6 s)=3.9 s`