Question

Solve the differential equation.

dy/dx = xy^2

Answer 1

`(dy)/(dx) = xy^2\ \Rightarrow\ (dy)/(y^2) = x \;dx\ [y \\e 0] \ \Rightarrow\ \int y^(-2) dy = \int x \, dx \Rightarrow \\ \\ -y^(-1) = (1)/(2)x^2 + C\ \Rightarrow\ (1)/(y) = -(1)/(2)x^2 - C \Rightarrow \\ \\ y = \displaystyle(1)/(-(1)/(2)x^2 - C) = (2)/(K - x^2),\ \text{where $K = -2C$}`

y = 0 is also a solution.

Answer 2

You can solve this differential equation by separating the variables and differentiating both sides.

1) Multiply both sides by dx and divide both sides by
`y^(2)`.

`(dy)/(dx) = xy^2\\ (1)/(y^2) \: dy = x\:dx`

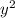
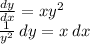
2) Integrate both sides. Remember the power rule for integrals. Say you have a value
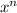
`x^(n)`, where
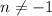
`n \\eq -1`. Take the power, n, and add 1. Then divide the new expression
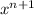
`x^(n+1)` by the new power, n + 1. The integral of
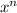
`x^(n)` would be
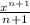
`(x^(n+1))/(n+1)` (+C, if it is an indefinite integral). Remember that you can subtract C from both sides and just have C on one side (since the constant doesn't have a definite value):

`(1)/(y^2) \: dy = x\:dx\\ \int (1)/(y^2) \: dy= \int x\:dx\\ \int y^(-2) \: dy= \int x\:dx \\ ( y^(-2+1))/(-2+1) + C = (x^(1+1))/(1+1) + C\\ - y^(-1) = ( x^(2))/(2) + C\\ -(2)/(y) = x^(2) + C\\ y = - (2)/(x^(2) + C)`

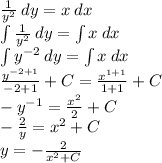Your solution is
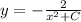`y = - (2)/(x^(2) + C)`.