Question

Find area of circle if circumference is 16.502

Answer 1

Hi there!

To find the area of a circle using the circumference you need to use the following formula:


`A= ( C^(2))/(4* \pi )`

Now to solve using this formula you need to plug in the circumference that you are given, which is 16.502:


`A= ( 16.502^(2))/(4* \pi )`

Now square the circumference to get:


`A= (272.316004)/(4* \pi )`

Now you want to multiply 4 by π to approximately get:


`A= (272.316004)/(12.566370)`

Now you want to divide 272.316004 by 12.566370 to get:


`\boxed {A=21.670220...}`

-Your friend, ASIAX

Answer 2

The equation for the circumference of a circle is
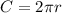
`C = 2 \pi r`, where C=circumference and r=radius of the circle.

You are told that the circumference is 16.502. Plug this into the equation for circumference to find the value of r, the radius:

`C = 2 \pi r\\ 16.502 = 2 \pi r\\ r = (16.502)/(2 \pi )`.

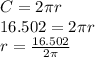
Now you know that r =
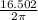
`(16.502)/(2 \pi )`. The equation for the area of a circle is
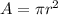
`A = \pi r^(2)`, where A = area and r = radius of the circle.

Since you know the radius, r =
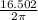
`(16.502)/(2 \pi )`, plug that into the equation for area and solve for the area of the circle:

`A = \pi r^(2)\\ A = \pi ((16.502)/(2 \pi ))^(2) \\ A \approx 21.670`

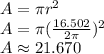
The area of the circle is about 21.670.