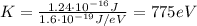Question

A proton traveling at 27.1° with respect to the direction of a magnetic field of strength 2.33 mt experiences a magnetic force of 6.54 × 10-17 n. calculate (a) the proton's speed and (b) its kinetic energy in electron-volts.

Answer 1

(a) The magnetic force experienced by a charged particle is:

`F=qvB \sin \theta`
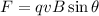
where
q is the charge
v is the velocity of the particle
B is the magnitude of the magnetic field

`\theta` is the angle between the directions of v and B

The proton in our problem has a charge of
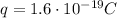
`q=1.6 \cdot 10^(-19) C`, and it travels through a magnetic field with strength

`B=2.33 mT=2.33 \cdot 10^(-3) T`
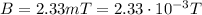
The direction between its velocity and B is
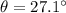
`\theta=27.1 ^(\circ)`, and the force exerted on the proton is
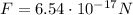
`F=6.54 \cdot 10^(-17)N`. Re-arranging the previous equation and using these data, we can find the value of v:

`v= (F)/(qB \sin \theta) = (6.54 \cdot 10^(-17)N)/((1.6 \cdot 10^(-19) C)(2.33 \cdot 10^(-3)T)(\sin 27.1^(\circ)))=3.85 \cdot 10^5 m/s`

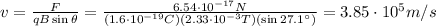
(b) Using the mass of the proton,
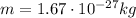
`m=1.67 \cdot 10^(-27)kg`, we find its kinetic energy:

`K= (1)/(2) mv^2= (1)/(2)(1.67 \cdot 10^(-27) kg)(3.85 \cdot 10^5 m/s)^2=1.24 \cdot 10^(-16) J`

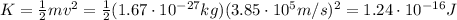
And keeping in mind that
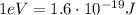
`1 eV = 1.6 \cdot 10^(-19)J`, we can convert this value into electronvolts:

`K= (1.24 \cdot 10^(-16) J)/(1.6 \cdot 10^(-19) J/eV)=775 eV`