Question

In a murder investigation, the temperature of a corpse was 32.5 degrees C at 1:30 pm and 30.3 degrees C an hour later. Normal body temperature is 37.0 degrees C and the temperature of the surroundings was 20.0 degrees C. When did the murder take place?

Answer 1

Let
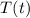
`T(t)` be the temperature of the body
`t` hours after 1:30 PM. Then
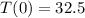
`T(0) = 32.5` and
`T(1) = 30.3`.

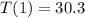
Using Newton's Law of Cooling,
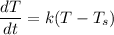
`(dT)/(dt) = k(T - T_s)`, we have
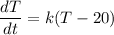
`(dT)/(dt) = k(T-20)`. Now let
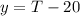
`y = T - 20`, so

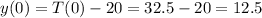
`y(0) = T(0) - 20 = 32.5 - 20 = 12.5`, so
`y` is a solution to the initial value problem
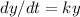
`dy/dt = ky` with
`y(0) = 12.5`.
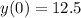
By separating and integrating, we have
`y(t) = y(0)e^(kt) = 12.5e^(kt)`.


`y(1) = 30.3 - 20\ \Rightarrow\ 12.5e^(k(1)) = e^(k) = (10.3)/(12.5)\ \Rightarrow \\ k = \ln (10.3)/(12.5)`


`y(t) = 37 - 20\ \Rightarrow\ 12.5e^(kt) = 17\ \Rightarrow\ e^(kt) = (10.3)/(12.5) \ \Rightarrow \\ \\ kt = \ln (10.3)/(12.5)\ \Rightarrow\ t = \left( \ln (17)/(12.5) \right)/ (10.3)/(12.5) \approx -1.588 \mathrm{\ h}`

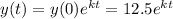
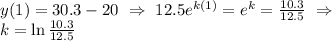
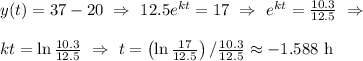
≈ 95 minutes. Thus the murder took place about 95 minutes before 1:30 PM, or 11:55 AM.