Question

A large grandfather clock strikes its bell once at 1:00, twice at 2:00, three times at 3:00, etcetera. what is the total number of times the bell will be struck in a day? use an arithmetic series to help solve the problem and show how you arrived at your answer.

Answer 1

There is a formula for adding consecutive integers.
sum = (n * (n+1)) / 2
for summing 1 through 12 it is
sum = (12 * 13) / 2 = 156/2 = 78
The clock goes through two "12-hour cycles" in a day, so the answer is 2 * 78 or 156 times.

Answer 2

300 times per day.

Explanation:

Basically, to solve this problem we just have to sum:

`1+2+3+...+24`

But, using an arithmetic series, we have to use this formula:

`Sum=n((a_(1)+a_(n) )/(2))`

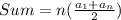
Where,
`n` is the total number of elements (in this case is 24),
`a_(1)` is the first element (1) and
`a_(n)` is the last element (24), because a day has 24 hours.

So, replacing all variables, we have:

`Sum=24((1+24)/(2))\\Sum=24(25)/(2)=300`

Therefore, the bell will be struck 300 times per day.