Question

Suppose that a large university contains 10 percent mountain climbers. if four students are randomly sampled from the university, find the probability that at least one student is a mountain climber. g

Answer 1

The probability to find at least one climber is the complement of the probability of finding none:
P(k ≥ 1) = 1 - P(k = 0)

In order to find P(k = 0) you need to use the binomial distribution:

`P(k) = (n!)/(k!(n-k)!) p^(k)(1 - p)^(n-k)`
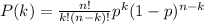
where:
n = total number of events
k = number of events we want successful
p = probability of success

Therefore:

`P(k=0) = (4!)/(0!(4-0)!) 0.1^(0)(1 - 0.1)^(4-0)`
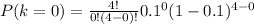
= (1 - 0.1)⁴
= 0.6561

Now you can calculate:
P(k ≥ 1) = 1 - P(k = 0)
= 1 - 0.6561
= 0.3439

Hence, the probability of finding at least one climber if four students are randomly sampled is 34.39%.