Solving this inequality is similar to solving a regular equation. The only thing you need to worry about with inequalities is that when you are dividing or multiplying by a negative number, you must flip the inequality sign. You won't have to worry about that here!
You are told x + 3/4 ≥ -1/3. Isolate the x by subtracting 3/4 from both sides. To subtract fractions, find a common denominator on both fractions, subtract the numerators, put the difference over the common denominator, and simplify if needed. The common denominator between
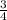
and
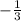
is 12.
1) To make the denominator of
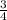
, 12, multiply it by 3/3 (aka 1):
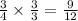
2) To make the denominator of
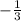
, 12, multiply it by 4/4:
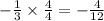
3) Subtract the fractions to find the inequality for x:
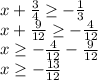
You answer is x ≥ -13/12, or if you want to make -13/12 a mixed number, x ≥
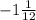
.