Answer:
Equation of image I is, y = 5x + 5
Explanation:
An Equation of line passing through the two points
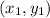 and
and
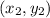 is given by;
is given by;
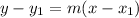 where m is the slope of the line.
where m is the slope of the line.
Given: Line I passes through the points (1, 6) and (-2, -9)
To find an equation of the image of I after a dilation of scale factor 5 centered at origin.
Dilation: A transformation in which a image grows larger. It may be with respect to a point or with respect to the axis of a graph.
Since, dilation requires a center point and a scale factor k.
The rule of dilation with a scale factor k =5 centered at origin is given by:
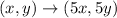
Now, to dilate the points of I are;
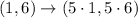 = (5 , 30)
= (5 , 30)
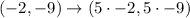 = (-10 , -45)
= (-10 , -45)
The points of image I are; (5, 30) and (-10 , -30)
First calculate the slope:
Slope(m) of the Image I is given by:
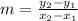
then;
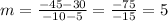
Then, the equation of image I is;
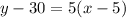
Using distributive property;
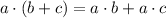
y -30 =5x -25
Add 30 to both sides we get;
y -30+30 = 5x -25 +30
Simplify:
y = 5x + 5
The equation of the image I after a dilation with scale factor of 5 centered at the origin is, y = 5x + 5