Question

Which function in vertex form is equivalent to f(x) = 4 + x2 – 2x?

f(x) = (x – 1)2 + 3
f(x) = (x – 1)2 + 5
f(x) = (x + 1)2 + 3
f(x) = (x + 1)2 + 5

Answer 1

A:

f(x) = (x – 1)2 + 3

Answer 2

To express a function of the form
`f(x)= x^(2) +bx+c` in vertex form
`f(x)=a(x-h)^2+k` where (h,k) is the vertex of the parabola, we need to find the vertex first.
To find the vertex we are going to use the vertex formula:
`h= (-b)/(2a)`, and
`k` will be the function evaluated at
`h`.
We can infer from our function that
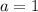
`a=1` and
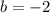
`b=-2`. So lets find
`h`:

`h= (-b)/(2a)`

`h= (-(-2))/(2(1))`

`h= (2)/(2)`

`h=1`
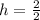
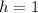
Now that we have
`h`, we can evaluate the function at 1 to find
`k`:

`f(x)=4+ x^(2) -2x`

`f(1)=4+(1)^2-2(1)`

`f(1)=4+1-2`

`f(1)=3`

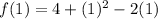
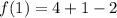
We have the vertex (1,3) of our parabola, so we can use its vertex form:

`f(x)=a(x-h)^2+k`

`f(x)=1(x-1)^2+3`

`f(x)=(x-1)^2+3`

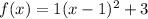
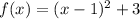
We can conclude that the vertex for of our parabola is f(x) = (x + 1)2 + 3.