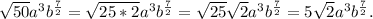Question

Which of the following is equal to square root 50a^6b^7?

Answer 1

5a^3b^3sqrt2b

Explanation:

I hope that makes sense I don't know how else to put it.

Answer 2

`5√(2)a^3b^{(7)/(2)}}.`

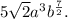
Explanation:

We need to calculate
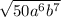`√(50a^6b^7)`. The properties of radicals say that a root of a product is a product of roots, i.e we can separate the root to each factor:

`√(50a^6b^7)=√(50)√(a^6)√(b^7).`

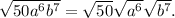
Now, another property of radicals says that if there is a root of one term with exponent, the result will be the term to the exponent divided by the root index, that is

`√(50)√(a^6)√(b^7)= √(50)a^{(6)/(2)}b^{(7)/(2)}= √(50)a^3b^{(7)/(2)}}.`

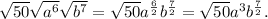
Finally, we can change the 50 to 25*2 to simplify:

`√(50)a^3b^{(7)/(2)}}= √(25*2)a^3b^{(7)/(2)}} =√(25)√(2)a^3b^{(7)/(2)}} = 5√(2)a^3b^{(7)/(2)}}.`