Question

If mCD= 118°, and AB = 66°, what is m∠CED? 90° 92° 66° 52°

Answer 1

Option B.

Explanation:

Consider the below figure attached with this question.

Given information: Measure of arc CD= 118°, and arc AB = 66°.

Angles of Intersecting Chords Theorem: If two chords intersect each other internally, then the angle between chords is half of the sum of major arc and minor arc.

Using the Angles of Intersecting Chords Theorem, we get

`\angle CED=(1)/(2)(Arc(CD)+Arc(AB))`

`\angle CED=(1)/(2)(118^(\circ)+66^(\circ))`

`\angle CED=(1)/(2)(184^(\circ))`

`\angle CED=92^(\circ)`

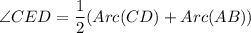
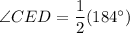
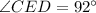
The measure of ∠CED is 92°. Therefore, the correct option is B.

Answer 2

Option
`m\angle CED=92\°`

Explanation:

we know that

The measure of the inner angle is the semi-sum of the arcs comprising it and its opposite.

see the attached figure to better understand the problem

`m\angle CED=(1)/(2)[arc\ CD+arc\ AB]`

substitute the given values

`m\angle CED=(1)/(2)[118\°+66\°]=92\°`