Question

Sara is completing the square to find the maximum or minimum value of the function f(x) = (2 - x) (5 + x). What is the first step that Sara must take? Does the function have a maximum or minimum value? What is that value?

A)multiply the binomials; maximum value; 49/4
B)multiply the binomials; minimum value; 49/4
C)set each factor equal to zero and solve for x; minimum value; −2/5
D)set each factor equal to zero and solve for x; maximum value; −7/2

Answer 1

That would be A
Maximum value of 49/4

Answer 2

Answer: The correct option is (A) multiply the binomials; maximum value;
`(49)/(4).`

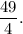
Step-by-step explanation: Given that Sara is completing the square to find the maximum or minimum value of the function below:

`f(x)=(2-x)(5+x).`

We are to find the first step that Sara take, the function will have whether maximum or minimum value. We are to find the value.

To find the maximum or minimum value, Sara need to differentiate the function and for that, first Sara will multiply the binomials (2 - x) and (5 + x).

So, the first step that Sara will take is that she will multiply the binomials.

We have,

`f(x)=(2-x)(5+x)\\\\\Rightarrow f(x)=10-3x-x^2.`

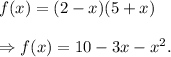
Differentiating the function, we have

`(d)/(dx)f(x)=(d)/(dx)(10-3x-x^2)\\\\\Rightarrow f^\prime(x)=-3-2x.`

Again differentiating, we have

`f^(\prime \prime)=(d)/(dx)(-3-2x)=-2<0.`

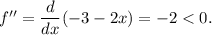
So, the function will have minimum value at

`f^\prime(x)=0\\\\\Rightarrow -3-2x=0\\\\\Rightarrow x=-(3)/(2).`

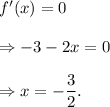
Therefore, the required maximum value of f(x) is

`f\left(-(3)/(2)\right)=10-3* \left(-(3)/(2)\right)-\left(-(3)/(2)\right)^2=10+(9)/(2)-(9)/(4)=(49)/(4).`

Thus, Sara will first multiply the binomial, the function has a maximum value, which is
`(49)/(4).`

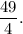
Thus, (A) is the correct option.