The correct answer is D.
In fact, the gravitational force exerted by the massive object on the less-massive object is equal to the force exerted by the less-massive object on the massive object, and it is equal to

where m is the mass of the less massive object, M the mass of the massive object, G the gravitational constant and r the distance between the two objects.
For Newton's second law, the force acting on each of the objects is the mass of the object times its acceleration:
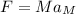

So the accelerations of the two objects are:
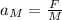
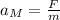
we can see from the two equations that
1) the acceleration of the massive object,
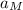
, is very small because its mass M is big
2) the acceleration of the less-massive object,
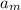
, is larger because its mass m is smaller
Therefore there will be a net acceleration produced on the less-massive object (and on the massive object, but it will be negligible)