Answer:
Explanation:
This is a permutation since order matters. We have 6 plates. Once we put a specific plate in position 1, we only have 5 plates left to fill the next position. After that, we only have 4 plates to fill the next position, and so on. The formula for that would look like this:
₆P₆ =
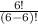 which simplifies to
which simplifies to
₆P₆ =
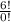 , where 0! = 1. Therefore, our formula comes down to
, where 0! = 1. Therefore, our formula comes down to
₆P6 = 6 * 5 * 4 * 3 * 2 * 1 which is 720
This is a factorial, also, where 6 * 5 * 4 * 3 * 2 * 1 is the number of different ways all 6 plates can be arranged. This is a total of 720 different ways to arrange them.