Question

What is (a) the wavelength of a 5.40-ev photon and (b) the de broglie wavelength of a 5.40-ev electron?

Answer 1

(a) for a photon, the relationship between frequency f and energy E is

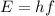
`E=hf` (1)
where h is the Planck cosntant.

First, we need to convert the energy from eV to Joule:

`E=5.40 eV \cdot (1.6 \cdot 10^(-19)J/eV)=8.6 \cdot 10^(-19) J`

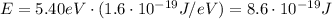
Then, using (1) we can find the frequency of the photon:

`f= (E)/(h)= (8.6 \cdot 10^(-19) J)/(6.6 \cdot 10^(-34)Js)=1.3 \cdot 10^(15) Hz`

and finally we can find its wavelength:

`\lambda = (c)/(f)= (3 \cdot 10^8 m/s)/(1.3 \cdot 10^(15)Hz) = 2.3 \cdot 10^(-7)m`

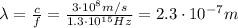
(b) now we have to find the De Broglie wavelength of an electron with same energy of the previous photon. Again, we must convert the energy in Joules first:

`E=5.40 eV \cdot (1.6 \cdot 10^(-19)J/eV)=8.6 \cdot 10^(-19) J`

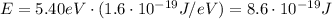
Then we can use the relationship between momentum p and energy E of a particle, to find p: (electron mass:
`m_e = 9.1 \cdot 10^(-31) kg` )

`E= (p^2)/(2m)`

`p= √(2Em)= \sqrt{2 (8.6 \cdot 10^(-19) J)(9.1 \cdot 10^(-31) kg)} =1.3 \cdot 10^(-24) kg m/s`

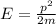
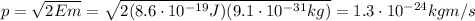
And finally we can use De Broglie relationship to find the wavelength of the electron:

`\lambda = (h)/(p) = (6.6 \cdot 10^(-34)Js)/(1.4 \cdot 10^(-24) kg m/s)=5.3 \cdot 10^(-10) m`