Question

Assume that male and female births are equally likely and that the birth of any child does not affect the probability of the gender of any other children. find the probability of exactly six boys in ten births. round the answer to the nearest thousandth.

Answer 1

The probability of exactly six boys in ten births is 0.0513.

Step-by-step explanation:

To find the probability of exactly six boys in ten births, we can use the binomial probability formula. The formula is:

`P(X=k) = C(n, k) * p^k * q^(n-k)`

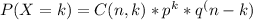
Where:

• P(X=k) is the probability of getting exactly k successes
• C(n, k) is the combination formula for choosing k items from a set of n items
• p is the probability of success (in this case, the probability of having a boy)
• q is the probability of failure (in this case, the probability of having a girl)
• n is the total number of trials or births
• k is the number of successes or boys

In this case, n=10 and p=q=1/2 because male and female births are equally likely. Therefore, the calculation would be:

`P(X=6) = C(10, 6) * (1/2)^6 * (1/2)^(10-6)`

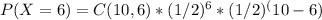
Simplifying the calculation:

P(X=6) = 210 * 1/64 * 1/64

`= 210/2^12`

= 210/4096

= 0.0513 (rounded to the nearest thousandth)

Answer 2

You need to use the binomial probability formula:

`p(k) = (n!)/(k!(n-k)!) p^(k) (1-p)^(n-k)`

where:
n = total number of events = 10
k = number of events we are testing = 6
p = probability of event happening = 0.5


`p(6) = (10!)/(6!(10-6)!) 0.5^(6) (1-0.5)^(10-6)`
= 210×0.015625×0.0625
= 0.205078

Hence, the probability of getting 6 boys out of 10 births is p = 0.205.