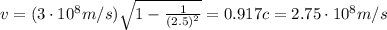Question

At what speed is a particle's momentum 2.5 times more than its newtonian value?

Answer 1

The relativistic momentum of a particle moving with speed v is equal to:

`p=\gamma m_0 v`
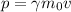
where

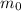
`m_0` is the rest mass of the particle

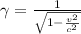
`\gamma= \frac{1}{ \sqrt{1- (v^2)/(c^2) } }` is the relativistic factor, with c being the speed of light.

The Newtonian momentum is instead

`p=m_0 v`

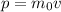
For the particle in our problem, the relativistic momentum is 2.5 times the Newtonian momentum: this means
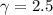
`\gamma=2.5`. If we re-arrange the formula of
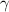
`\gamma`, we get:

`v=c \sqrt{1- (1)/(\gamma^2) }`
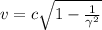
and by using
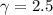
`\gamma=2.5`, we find the particle velocity:

`v=(3 \cdot 10^8 m/s) \sqrt{1- (1)/((2.5)^2)} =0.917 c = 2.75 \cdot 10^8 m/s`