Question

The average estimated hours a person in the United States spent playing video games per year from 2002 to 2012 were 71, 80, 82, 78, 80, 91, 107, 121, 125, 131, and 142. Use the statistics calculator to find the variance and population standard deviation. Round answers to the nearest whole number.

Answer 1

Population variance 579

Population standard deviation 24

Explanation:

The average estimated hours a person in the United States spent playing video games per year from 2002 to 2012 were 71, 80, 82, 78, 80, 91, 107, 121, 125, 131, and 142.

The population variance is given by:

`\sigma^2=(\sum(x-\mu)^2)/(n)`

`\mu=(71+80+82+78+80+91+107+121+125+131+142)/(11)`

`\mu=(1108)/(11)`

This implies that:

`\sigma^2=((71-(1108)/(11))^2+(80-(1108)/(11))^2+(82-(1108)/(11))^2+(78-(1108)/(11))^2+(80-(1108)/(11))^2+...+(142-(1108)/(11))^2)/(11)`

`\sigma^2=(70006)/(121) =579` to the nearest whole number

The population standard deviation is

`\sigma=(√(70006) )/(11)=24` to the nearest whole number.

Answer 2

Variance = 579 and Standard deviation = 24

Explanation:

The given data set is the average estimated hours of a person in the U.S. spent playing video games per year from 2002 to 2012.

71, 80, 82, 78, 80, 91, 107, 121, 125, 131, 142.

We have to find the variance and standard deviation.

Formula for standard deviation :

`\sqrt{\frac{\sum (x-\bar{x})}{n}}`

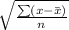
Using the step by step approach to find the standard deviation.

1. Calculate the mean

`\bar{x}=(\sum x)/(n)`

=
`(1108)/(11)`

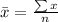
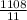
= 100.73

2. Subtract the mean from each value and square them then add all the squared result.

Time (x)
`x-\bar{x}`
`(x-\bar{x})^(2)`

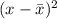
71 -29.73 883.8729

80 -20.73 429.7329

82 -18.73 350.8129

78 -22.73 516.6529

80 -20.73 429.7329

91 -9.73 94.6729

107 6.27 39.3129

121 20.27 410.8729

125 24.27 589.0329

131 30.27 916.2729

142 41.27 1,703.2129

6,364.1819

3. To calculate Variance (S²) divide this number by the total number of the data

Variance (S²) =
`(6364.1819)/(11)`

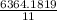
Variance = 578.56 ≈ 579

4. For standard deviation

Standard deviation =
`√(579)`

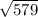
= 24.0624188 ≈ 24

Variance = 579 and Standard deviation = 24