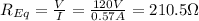Question

A string of 27 identical christmas tree lights are connected in series to a 120 v source. the string dissipates 68 w. what is the equivalent resistance of the light string? answer in units of ω.

Answer 1

The power dissipated by the whole string of tree lights is:

`P= VI`
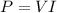
where
V is the potential difference of the whole circuit
I is the current flowing through the tree lights.

By using P=68 W and V=120 V, we find the current:

`I= (P)/(V)= (68 W)/(120 V)=0.57 A`

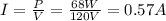
Ohm's law for the whole string of tree lights is:

`V=IR_(eq)`
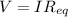
where
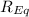
`R_(Eq)` is their equivalent resistance. Re-arranging the equation, we find the value of the equivalent resistance:

`R_(Eq)= (V)/(I)= (120 V)/(0.57 A)=210.5 \Omega`