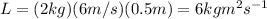Question

A 2 kg stone is tied to a 0.5 m string and swung around a circle at a constant angular velocity of 12 rad/s. the angular momentum of the stone about the center of the circle is:

Answer 1

Starting from the angular velocity, we can calculate the tangential velocity of the stone:

`v=\omega r= (12 rad/s)(0.5 m)= 6 m/s`

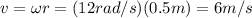
Then we can calculate the angular momentum of the stone about the center of the circle, given by

`L=mvr`
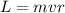
where
m is the stone mass
v its tangential velocity
r is the radius of the circle, that corresponds to the length of the string.

Substituting the data of the problem, we find

`L=(2 kg)(6 m/s)(0.5 m)=6 kg m^2 s^(-1)`