Answer:
1620 years
Explanation:
Given : Radium-226 is a radioactive element, and its decay rate is modeled by the equation R = R0e-0.000428t
Solution:
We will find total number of particles in 100 gram sample :
Ro = 100 grams * 1 mol / 226 g = 0.4425 mol
Now we will find total number of particles when the 100 gram sample is reduced to half its mass:
R = Ro/2 = 0.4425/2 = 0.2212
On substituting values of Ro and R to the decay rate equation, we get
R = Ro e^-0.000428t
0.2212 = 0.4425 e^-0.000428t
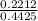 = e^-0.000428t
= e^-0.000428t
Now, take natural logarithm on both sides of the equation in order to find value of t .
ln (0.2212/0.4425) = -0.000428t
t= ln (0.2212/0.4425) / (-0.000428)
t = 1620 years