Question

You are a member of your local movie theaters club. every time you see a movie at the theater, you earn 2 advantage points. When you earn 100 points, you can get a free movie pass. currently you have 40 advantage points. Write an equation to model the number of movies (m) you have to watch before you earn a free movie pass. solve the equation and show your work.

Answer 1

30 movies.

Explanation:

Hey! Let's help you with your question here!

Alright, so here's what we know. When we go see a movie, we earn 2 advantage points. We need 100 points to get a free movie pass and we currently have 40 advantage points.

When writing equations like this, we need to know what the fixed values and the variable values are. The variable values are subject to change, where the fixed values, we cannot change.

In this question here, we have 40 advantage points and this is already given to us, so it cannot change. This is our fixed value. What we can change is how many times we can see a movie after that, which will earn us 2 advantage points each time. This will be our variable value.

Now that we've determined our values, let's create the formula! I will be using y to represent the total amount of points and m to represent the amount of movies seen. So, we write it as such:

`y=2(m)+40`

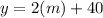
We got our formula! Now we have to figure out how many more movies we need to watch to get our free movie pass. Since we know that is the total amount of points that we need to get, we can substitute 100 into y to solve for m which is the number of movies! It would look like this:

`100=2(m)+40`

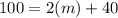
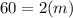`60=2(m)` - We move 40 over to the left side and subtracted 100 by 40.

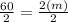`(60)/(2)=(2(m))/(2)` - We divide both sides by 2 to get rid of the 2 in front of the m.

`30=m`

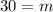
And there we have it! We would need to see 30 movies in order to get our free movie pass! You can double check this by taking
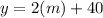`y=2(m)+40` and substitute m with 30 and find y.