Question

Calvin purchases a piece of heavy machinery for $32,300. The value of the machine depreciates at an annual rate of 8.3% . Which function of represents the value of the machine with an approximate equivalent monthly depreciation rate?

Answer 1

32,300 / 8.3 = x , how much value it loses monthly.
x = $3891.56627

Answer 2

Calvin purchases a piece of heavy machinery for $32,300. The value of the machine depreciates at an annual rate of 8.3%

Annual depreciation rate = 8.3% =
`(83)/(100) = 0.083`

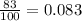
For monthly depreciation rate we we raise to the exponent
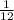`(1)/(12)`. Also we multiply the number of years by 12.

We know depreciation formula is

`A = p (1 - r)^t`

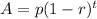
Where 'p' is the initial cost, 'r' is the annual depreciation rate and 't' is the number of years

Here p = 32,300

r = 0.083 for monthly we raise to the exponent
`(1)/(12)`

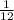
so
`(1-r)(1)/(12)^`

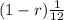
t= number for years , for monthly we put 12t

So equation becomes

`A = 32300 ( (1-0.083)^(1)/(12) )^(12t)`

`A = 32300 ( 0.917^(1)/(12) )^(12t)`

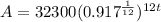
function of represents the value of the machine with an approximate equivalent monthly depreciation rate is

`f(t) = 32300 ( 0.917^(1)/(12) )^(12t)`