Question

The general form of the equation of a circle is x^2+y^2−8x+6y+21=0.

What are the coordinates of the center of the circle?



Enter your answer in the boxes.

(_____,______)

Answer 1

the anwser is (4,-3)

Answer 2

The coordinates of the center of the circle are (4,-3).

Explanation:

The general form of the equation of a circle is

`x^2+y^2-8x+6y+21=0`

It can be written as

`(x^2-8x)+(y^2+6y)+21=0`

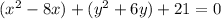
Add and subtract
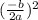`((-b)/(2a))^2` in each parenthesis, to make perfect squares.

For first parenthesis,

`((-b)/(2a))^2=(frac{8}{2(1)})^2=(4)^2=16`

For second parenthesis,

`((-b)/(2a))^2=(frac{-6}{2(1)})^2=(-3)^2=9`

`(x^2-8x+16-16)+(y^2+6y+9-9)+21=0`

`(x^2-8x+16)+(y^2+6y+9)+21-16-9=0`

`(x-4)^2+(y+3)^2-4=0`

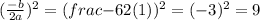
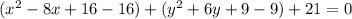
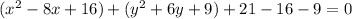
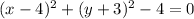
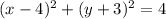`(x-4)^2+(y+3)^2=4` .... (1)

The standard form of a circle is

`(x-h)^2+(y+k)^2=r^2` .... (2)

Where, (h,k) is center of the circle and r is radius.

On comparing (1) and (2) we get,

`h=4,k=-3,r=2`

Therefore the coordinates of the center of the circle are (4,-3).