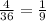Question

A single die is rolled twice. the 36​ equally-likely outcomes are shown to the right. find the probability of getting two numbers whose sum is 5.

Answer 1

Total possible outcome = 36

Outcome with sums is 5 = 4
{1, 4} (2, 3} {3, 2} {4, 1}

P(getting sum = 5) = 4/36 = 1/9

Answer: 1/9

Answer 2

Given: A single die is rolled twice.

To Find: Probability of getting two numbers whose sum is 5.

Solution: The required probability is \frac{1}{9}[/tex]

Step-by-step explanation:

When we roll a die once, there are 6 possible outcomes.

When we roll the same die once again, there will be a total of 6*6=36 possible outcomes.

This is the set of total possible outcomes

Now let us see the number of outcomes of getting two numbers whose sum is 5. This is possible when a 1 and 4 are rolled (1,4) and (4,1) or when a 2 and 3 are rolled (2,3) and (3,2).

Thus, there are 4 possible outcomes for this.

Therefore the probability will be
`(4)/(36)= (1)/(9)`