Answer:
t = 21.5 min.
Step-by-step explanation:
Hello!
In this case, since the kinetics of a first-order reaction is:
![([A])/([A]_0)=exp(-kt)](https://img.qammunity.org/2022/formulas/chemistry/college/u2ixctzq6z8cx5qq1ochdnsxpzxwxa40an.png)
Thus, since we are given the 11.7 min for a 58.6-% consumption, we can compute the rate constant, k:
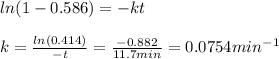
Now, for the second problem, as the new consumption is 80.2%, we can compute the required time as shown below:
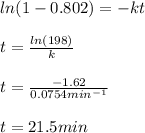
Best regards!