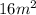Answer:
Option b is correct
16
Explanation:
Area of circle (A) is given by:
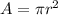
where, r is the radius of the circle.
As per the statement:
the areas of a circle with diameter 4 m
Formula for Diameter(d) is:
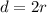
⇒
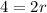
Divide both sides by 2 we get;
r = 2 m
then;

It is also given: a circle with diameter 6 m
Similarly;

⇒
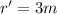
then;
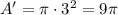
We have to find the difference in these areas:
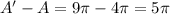
Use
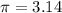
then;

Therefore, the difference in the areas of a circle with diameter 4 m and a circle with diameter 6 m is,