Answer:
Option B - No. P(S∩F) = 6% and P(S)·P(F) = 2.4%
Explanation:
Given : In a school of 1250 students, 250 are freshmen and 150 students take Spanish. The probability that a student takes Spanish given that he/she is a freshman is 30%.
To find : Are being a freshman and taking Spanish independent?
Solution :
Two events A and B are independent if
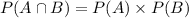
We have given,
Total number of students = 1250
Students take Freshmen F = 250
Students take Spanish S= 150
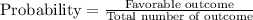
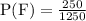
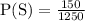
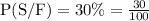
To show,
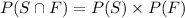
Now, Taking LHS
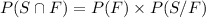
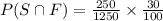
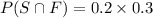
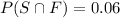
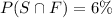
Now, Taking RHS
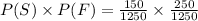
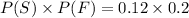
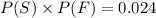
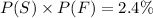
Since,
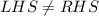
Being a freshman and taking Spanish are not independent.
Therefore, Option B is correct.
No. P(S∩F) = 6% and P(S)·P(F) = 2.4%