Answer:
OptionC
Explanation:
A circle A has radius 6m.
One sector has area as 10 pi m^2
central angle = 100 degrees
Area of the sector =
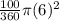
Area of sector in circle B =
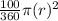
where r=radius of circle B
Hence ratio of these would be the ratio of square of radii
i.e.

So radius of circle B = 12m
Option C is right