Answer:
B. 2
Step-by-step explanation:
From the graph we get
(1).
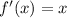 for
for
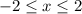
(2).
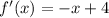 for
for
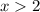
(3).
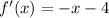 for
for
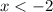
Now let us take the anti derivative of the second function, and we get
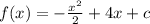 for
for
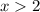
We find
 from the condition
from the condition
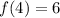 :
:

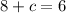

Thus we have
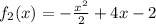 .
.
Now we find the anti derivative of the first function, and get
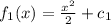
What we note now is that the function is continuous because the derivative of the functions is defined at
 and at
and at
 .
.
since the function are continuous,
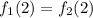
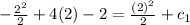

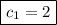
Thus we have
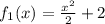
Now we can easily evaluate
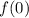
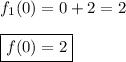
Which is choice B.