Question

Determine whether the following sequence is arithmetic, geometric, or neither.

1, 2, 2, 3, ...

arithmetic
geometric
neither

Answer 1

The following sequence shown up top is arithmetic sequence

Answer 2

Answer: neither

Explanation:

Consider sequence
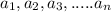`a_1 , a_2 , a_3 , .....a_n`, where n acn be any natural number.

This sequence is said to be Arithmetic sequence if the difference between two consecutive terms is equal.

i.e, if it is arithmetic then
`d=a_2-a_1=a_3-a_2=...=a_n-a_(n-1)`

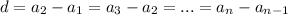
This sequence is said to be Geometric sequence if the common ratio between two consecutive terms is equal.

`r=(a_2)/(a_1)=(a_3)/(a_2)=......=(a_n)/(a_(n-1))}`

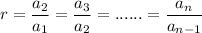
The given sequence = 1, 2, 2, 3, ...

Here ,
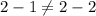`2-1\\eq2-2` , so difference between two consecutive terms is not equal.

⇒ Its not an Arithmetic sequence.

Also ,
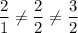`(2)/(1)\\eq(2)/(2)\\eq(3)/(2)`, so ratio between two consecutive terms is also not equal.

⇒ Its not an Geometric sequence.

Hence, the given sequence is neither arithmetic nor geometric.