Question

Please help, algebra, 90 points!

factor 4x²+20x

factor x²+9x+8

solve 4r² -16=84

find the solution to the following equation by transferring it into a perfect square trinomial x²-6x=27

use the quadratic formula to solve 3y²-9y-30=0

where is the vertex of the parabola
y=x^2+6x+7

in which direction does the parabola open? y=3x²+5x+10

Answer 1

You have a lot of questions here, I will help with the first three:

Factor:

4x^2 + 20x Factor out a 4x
4x(x + 5)

x^2 + 9x + 8 You have to work backwards with FOIL here
(x + 1)(x + 8)


Solve:

4r^2 - 16 = 84
4r^2 = 100
r^2 = 25

r = 5 or r = -5

Answer 2

#1: 4x(x+5)
#2: (x+8)(x+1)
#3: r=5
#4: x=9
#5: y=-2 or y=5
#6: (-3, -2)
#7: It opens upward.

To factor #1, pull out what each has in common; both are divisible by 4 and both have an x, so pull 4x out:
4x(x+5)

To factor #2, find factors of c (8) that sum to b (9). The only factors of 8 that will sum to 9 are 8 and 1:
(x+8)(x+1)

To complete the square on #3, we divide b by 2 and square it: (-6/2)² = (-3)² = 9. Add this to both sides:
x²-6x+9=27+9
(x-3)²=36

Take the square root of both sides, and we have
x-3=6
x = 9

Using the quadratic on #4,

`x=(-b\pm √(b^2-4ac))/(2a) \\ \\y=(--9\pm √((-9)^2-4(3)(-30)))/(2(3)) \\ \\=(9\pm √(81--360))/(6)=(9\pm √(441))/(6) \\ \\=(9+21)/(6)\text{ or }(9-21)/(6)=(30)/(6)\text{ or }(-12)/(6) \\ \\=5\text{ or }-2`

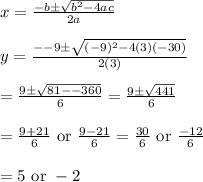
To find the vertex on #5, use x=-b/2a:
x = -6/2(1) = -6/2 = -3

Now substitute this back into the equation to solve for y:
y=(-3)²+6(-3)+7=9-18+7=-2

This makes the vertex (-3, -2)

For #6, it opens upward since the coefficient of a is positive.