Answer:
The water level is changing at - 0.016 centimeters per minute when the water is 10 centimeters deep.
Explanation:
From Geometry, the volume of the cone (
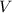 ), measured in cubic centimeters, is defined by:
), measured in cubic centimeters, is defined by:
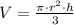 (1)
(1)
Where:
 - Radius, measured in centimeters.
- Radius, measured in centimeters.
 - Height, measured in centimeters.
- Height, measured in centimeters.
Then, we find a formula for the rate of change of the volume of the birth bath (
 ), measured in cubic centimeters per minute, by means of differentiation:
), measured in cubic centimeters per minute, by means of differentiation:
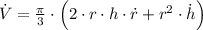 (2)
(2)
Where:
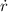 - Rate of change of radius, measured in centimeters per minute.
- Rate of change of radius, measured in centimeters per minute.
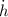 - Rate of change of height, measured in centimeters per minute.
- Rate of change of height, measured in centimeters per minute.
In addition, we have the following relationship:
 (3)
(3)
And by Differential Calculus:
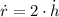 (4)
(4)
By applying (3) and (4) in (2), we find the following expanded formula:
![\dot V = (\pi)/(3)\cdot \left[2\cdot (2\cdot h)\cdot (2\cdot \dot h)+4\cdot h^(2)\cdot \dot h\right]](https://img.qammunity.org/2022/formulas/mathematics/college/dhy92cne0fufm69gletuogs70rtaygczwu.png)
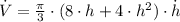 (5)
(5)
If
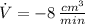 and
and
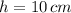 , then the rate of change of the water level is:
, then the rate of change of the water level is:
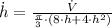
![\dot h = (-8\,(cm^(3))/(min) )/((\pi)/(3)\cdot [8\cdot (10\,cm)+4\cdot (10\,cm)^(2)] )](https://img.qammunity.org/2022/formulas/mathematics/college/4r4gg5u12eerx9z12q26mfhhkzer4mmmnd.png)
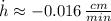
The water level is changing at - 0.016 centimeters per minute when the water is 10 centimeters deep.