Hey there :)
Right triangle pennant with
Hypotenuse = 10 ft
One side is 2 ft longer than other = 2 + p
Other side = p
Since it is a right triangle, we can solve by Pythagoras Theorem:
( Side 1 )² + ( Side 2 )² = ( Hypotenuse )²
( p )² + ( 2 + p )² = ( 10 )²
↓ Solve by FOIL ( First, Outer, Inner, Last )
2 ( 2 ) + 2 ( p ) + 2 ( p ) + p ( p ) = 4 + 4p + p²
p² + 4 + 4p + p² = 100
Take 100 to left hand side and equate to 0 and add like-terms together
2p² + 4p + 4 - 100 = 0
2p² + 4p - 96
Divide the whole equation by 2 for simplified form
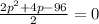
p² + 2p - 48
Factorise { Sum = 2 , Product = - 48 } Therefore, possible factors 8 and - 6
( p - 6 )( p + 8 ) = 0
p = 6 , p = - 8
↑ ↑
↑ A length can never be negative
One length = 6 ftOther length = 2 + 6 = 8 ft