Question

If y= 3x + 6, what is the minimum value of (x^3)(y)?

Answer 1

Given the statement: if y =3x+6.

Find the minimum value of
`(x^3)(y)`

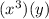
Let f(x) =
`(x^3)(y)`

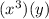
Substitute the value of y ;

`f(x)=(x^3)(3x+6)`

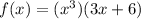
Distribute the terms;

`f(x)= 3x^4 + 6x^3`

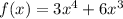
The derivative value of f(x) with respect to x.

`(df)/(dx) =(d)/(dx)(3x^4+6x^3)`

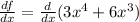
Using
`(d)/(dx)(x^n) = nx^(n-1)`

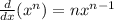
we have;

`(df)/(dx) =(12x^3+18x^2)`

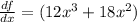
Set
`(df)/(dx) = 0`

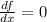
then;

`(12x^3+18x^2) =0`

`6x^2(2x + 3) = 0`

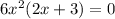
By zero product property;

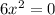`6x^2=0` and 2x + 3 = 0

⇒ x=0 and x =
`-(3)/(2) = -1.5`

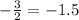
then;

at x = 0

f(0) = 0

and

x = -1.5

`f(-1.5) = 3(-1.5)^4 + 6(-1.5)^3 = 15.1875-20.25 = -5.0625`

Hence the minimum value of
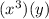`(x^3)(y)` is, -5.0625