Question

The vertex angle of an isosceles triangle is 20° less than the sum of the base angles. Which system of equations can be used to find the measure of the vertex and base angles?

Answer 1

The base angles are equal and we'll call those "x" and "x".
We'll call the vertex angle y.
A) y + 2x = 180
B) y + 20 = 2x we can algebraically shift "B)" into
B) y - 2x = -20 then we'll add that to "A)"
A) y + 2x = 180
2y = 160
"y" the vertex angle = 80 degrees
each base angle = 50 degrees

Answer 2

The vertex angle is 80°, and each base angle is 20°.

Explanation:

By definition, we know that the angles of the base of an isosceles triangle are equal.

"The vertex angle of an isosceles triangles is 20° less than the sum of the base angles" this expression can be expressed like

`V=B+B-20\°`

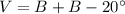
Where
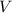`V` is the vertex angle and
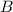`B` represents each base angle.

Also, we use the theorem which states that the sum of all interior angles of a triangle is equal to 180°, that is

`V+B+B=180\°`

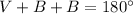
Now, to find each angle, we replace the first expression into the second one and solve for
`B`

`B+B-20\°+B+B=180\°\\4B=180\°+20\°\\B=(200\°)/(4)\\ B=50\°`

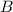
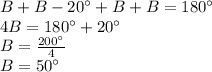
Then, we replace this value in one equation to find the other value

`V=50\°+50\°-20\°=80\°`

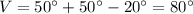
Therefore, the vertex angle is 80°, and each base angle is 20°.