Question

QUESTION

Your Assignment: Profit from Sales
You are deciding how much to charge for an item you want to sell. To answer these questions, you will factor a polynomial expression to find the break-even points, or the prices at which your profit from sales will be 0.
1. Circle the item that you want to sell.



T-shirts Hats Water bottles
Making Sense of the Problem
Make Sense of the Problem
What do you know?



What do you want to find out?



What kind of answer do you expect?



3. Fill in the blanks. (1 point)

The profit expression is __________________.


4. Set the profit expression as an equation equal to 0. (1 point)

____________________ = 0


5. Factor out the coefficient of the squared term. (2 points)






6. Factor the remaining trinomial. (4 points: 2 points for each factor)






7. If a product is equal to 0, then at least one of the factors must be 0. The constant factor cannot be 0. Set each binomial factor equal to 0 and solve for the variable. (2 points: 1 point for each factor)








8. Use your answer from question 7 to identify the two break-even points. (1 point)

You will make a profit if you sell your item for between $_______ and $_________.


9. Check your work. Substitute each value into the equation from question 4 to confirm that it makes the expression equal to 0. (2 points: 1 point for each value)












10. Below are the graphs for the profit functions. Write the coordinates of the highest point on the graph for your item. (1 point)

(____, ____).



11. The x-value of the point from question 10 is the price that will give you the maximum profit. The y-value of the point is the maximum profit that you can make. (3 points)

PROMPT
Transcript: Modeling: Factoring Polynomials

This interactive animation shows an image of a basketball game between two teams. The title "Profit from Sales" is shown and a "Begin" button starts the animation. [Click "Begin."]

On-screen text and Audio:

Profit from Sales: You're setting up a table at a basketball game to sell items to raise money for the Student Association. There are costs associated with buying the items. After you pay these costs, the profit, or money you make, will depend on the price the item sells for. You need to decide how much to charge. First, pick an item that you want to sell. [An image of a grey T-shirt, a water bottle, and a black hat can be seen on the screen. Any of the images can be clicked and a message pops up.]

T-shirts: Great! You've decided to sell T-shirts. The expression –2t2 + 60t – 250 represents your profit when the price of a T-shirt is t dollars.

The break-even points are the prices at which your profit will be 0. Write an equation by setting the above expression equal to 0. Then factor the expression to find the break-even points for this item.

Water bottles: Great! You've decided to sell water bottles. The expression –10w2 + 100w – 90 represents your profit when the price of a water bottle is w dollars.

The break-even points are the prices at which your profit will be 0. Write an equation by setting the above expression equal to 0. Then factor the expression to find the break-even points for this item.

Hats: Great! You've decided to sell hats. The expression –3h2 + 66h – 120 represents the profit for the hats when the price of a hat is h dollars.

The break-even points are the prices at which your profit will be 0. Write an equation by setting the above expression equal to 0. Then factor the expression to find the break-even points for this item.

Answer 1

200 LOL

Explanation:

Answer 2

1. The answer to this item will depend on your personal preference. The given polynomial for all three options do not vary greatly therefore difficulty won't be an issue. For this answer let's pick T-shirts as the one we are going to sell.

2a. What do you know?
We know the expression that represents our profit for every price of the T-shirt. This polynomial expression is given by
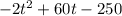
`-2t^(2)+60t-250`. In this expression t is the price of a single T-shirt in dollars while the entire expression represents the profit.

2b. What do you want to find out?
We want to find out the price points where our profit will be zero (or where we would break-even). Therefore, we just need to equate the expression given in the previous question to zero, since this would mean that we are setting the profit to zero.

2c. What kind of answer do you expect?
We expect the answer to be in dollars (the price of the T-shirt). The expression is in quadratic form so we would also be expecting two roots. Both these roots will still be in dollars and they will both be valid. The reason we have two is because our profit will start small for a small price, increase, and finally decrease as our price becomes too expensive. These two roots will then be the range where our profit would be positive.

3. You can approach this item by simply looking at what has been given. We have also already mentioned the expression for the profit above. We just copy this expression to complete the sentence.

The profit expression is
`-2t^(2)+60t-250`.

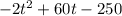
4. This item is basically telling us to do the same as in item #3. The only thing that we need to do in this step is to copy the profit expression again and equate it to zero. Given the previously identified expression, we'll have the answer:


`-2t^(2)+60t-250=0`

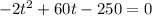
5. What this means is that we simply need to divide the equation by the coefficient of the squared term and factor out this coefficient. We can see that the coefficient is -2, thus we just also divide 60 and -250 by -2 so we can factor it out.


`-2(t^(2)-30t+125)=0`

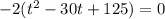
6. To factor the trinomial completely, we just figure out the possible factors of the quadratic equation. You can do this by trying out all factors of 125 that will have a sum of -30 (since 125 is the constant and -30 is the coefficient of t). Upon examining you should end up with:


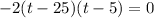
`-2(t-25)(t-5)=0` (Notice that -25 and -5 are factors of 125 and their sum is -30.)

7. The rule stated on this item just means that we can equate each individual factor to zero (except for the constant term) to find out the possible values of t. That means that we can solve for t by using the equations t-25=0 and t-5=0.


`t-25=0`

`t=25`


`t-5=0`

`t=5`

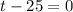
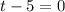
8. This question is straight-forward. Now that you have found the roots of the equation, all you need to do is to correctly interpret them. Recall that the equation represented the point where our profit will be zero (break-even), and t is the price of the shirt. That means the values that we got represent the price points where we won't have any profit. (And as I said before, you will only make a profit between these two break-even points since a price that is too low would be undercharging and a price that is too high would be too expensive.)

You will make a profit if you sell your item for between $5 and $25.

9. For this item, we just do simple substitutions to the equation to verify whether the values we got in question 7 is really a solution to the equation. The values of t that we got are 5 and 25 so we substitute these one at a time.


`-2(5)^(2)+60(5)-250=0`

`-50+300-250=0`

`0=0`


`-2(25)^(2)+60(25)-250=0`

`-1250+1500-250=0`

`0=0`

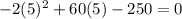
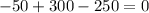
Both values of t make the left side equal to zero therefore both are solutions to the equation.

10. For this item we just look at the graphs you attached. We pay particular attention to the graph of the T-shirts. This is the first image among the attachments. The highest point of the graph is already plotted out for us, we just need to copy the coordinates.

It's the coordinates (15,200).

11. This item is asking us to interpret the highest point of the graph that we have answered in item #10. The explanation for these coordinates are already given in the item. The x-coordinate is the price that would give us the maximum profit while the y-coordinate is the maximum profit that we can make.

Based on this description, we can tell that we should sell the T-shirts at $15 so we could have the maximum profit which is $200.