Question

The formula for determining the frequency, f, of a note on a piano is f=440(2)^h/12 where h is the number of half-steps from the A above middle C on the keyboard. A note is six half-steps away from the A above middle C. The frequency of the A above middle C is 440 Hz. How much greater is the frequency of the new note compared with the frequency of the A above middle C?

A)29.3%
B)41.4%
C)70.7%
D)182.3%

Answer 1

How much greater is the frequency of the new note compared with the frequency of the A above middle C?

• 29.3%
• 41.4% <<<CORRECT
• 70.7%
• 182.3%

Explanation:

Edge2021

Answer 2

Option B - 41.4%

Explanation:

Given : The formula for determining the frequency, f, of a note on a piano is
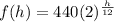`f(h)=440(2)^{(h)/(12)}` where h is the number of half-steps from the A above middle C on the keyboard.

A note is six half-steps away from the A above middle C. The frequency of the A above middle C is 440 Hz.

To find : How much greater is the frequency of the new note compared with the frequency of the A above middle C?

Solution : The formula for determining the frequency
`f(h)=440(2)^{(h)/(12)}`

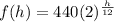
When the note is at initial stage i.e, h=0 frequency is

`f(0)=440(2)^{(0)/(12)}`

`f(0)=440(1)`

`f(0)=440`

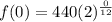
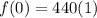
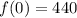
A note is six half-steps away from the A above middle C i.e, h=6

`f(6)=440(2)^{(6)/(12)}`

`f(6)=440(2)^(1)/(2)`

`f(6)=440(1.41)`

`f(6)=622.25`

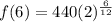
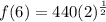
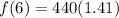
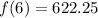
Initial frequency is 440 hz.

Final frequency is 622.25 hz.

To find change formula is

`=\frac{\text{final} - \text{initial}}{\text{Initial}}`

`=(622.25- 440)/(440)`

`=0.414`

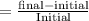
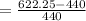
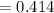
Frequency change in percentage

`0.414* 100= 41.4\%`

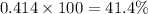
Therefore, Option B is correct.