Question

The coefficients of friction between the load and the flatbed trailershown are μs = 0.40 and μk = 0.30. Knowing that the speed of the rigis 72 km/h, determine the shortest distance in which the rig can bebrought to a stop if the load is not to shift

Answer 1

50.97 m

Step-by-step explanation:

m = Mass of truck

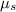`\mu_s` = Coefficient of static friction = 0.4

v = Final velocity = 0

u = Initial velocity = 72 km/h =
`(72)/(3.6)=20\ \text{m/s}`

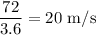
s = Displacement

Force applied

`F=ma`

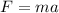
Frictional force

`f=\mu_s mg`

Now these forces act opposite to each other so are equal. This is valid for the case when the load does not slide

`ma=\mu_s mg\\\Rightarrow a=\mu_s g\\\Rightarrow a=0.4* 9.81\\\Rightarrow a=3.924\ \text{m/s}^2`

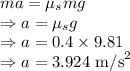
Since the obect will be decelerating the acceleration will be
`-3.924\ \text{m/s}^2`

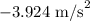
From the kinematic equations we have

`v^2-u^2=2as\\\Rightarrow s=(v^2-u^2)/(2a)\\\Rightarrow s=(0^2-20^2)/(2* -3.924)\\\Rightarrow s=50.97\ \text{m}`

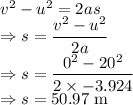
So, the minimum distance at which the car will stop without making the load shift is 50.97 m.