Question

A father fashions a swing for his children out of a long rope that he fastens to the limb of a tall tree. As one of the children swings from this rope that is 6.00 m long, his tangential speed at the bottom of the swing is 9.50 m/s. What is the centripetal acceleration, in m/s2, of the child at the bottom of the swing

Answer 1

10.8n

Step-by-step explanation:

For this case the centripetal force is given by:

Where,

m: mass of the object

v: tangential speed

r: rope radius

Substituting values in the equation we have:

Then, doing the corresponding calculations:

Answer:

The centripetal force exerted on the rope is:

Answer 2

The centripetal acceleration of the child at the bottom of the swing is 15.04 m/s².

Step-by-step explanation:

The centripetal acceleration is given by:

`a_(c) = (v^(2))/(r)`

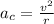
Where:

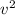`v^(2)`: is the tangential speed = 9.50 m/s

r: is the distance = 6.00 m

Hence, the centripetal acceleration is:

`a_(c) = (v^(2))/(r) = ((9.50 m/s)^(2))/(6.00 m) = 15.04 m/s^(2)`

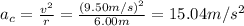
Therefore, the centripetal acceleration of the child at the bottom of the swing is 15.04 m/s².

I hope it helps you!