Question

Mark deposits $12,000 into an account that pays 4% interest, compounded annually, for 5 years. Saul deposits $10,000 into an account that pays 6% interest, compounded annually, for 8 years. Assuming no additional deposits are made, compare the interest earned on the accounts at the end of the interest period for each. (to the nearest dollar)

A) Each account earned the same amount of interest.
B) Mark's account earned $40 more interest than Saul's account.
C) Saul's account earned $3,338 more interest than Mark's account.
D) Saul's account earned $1,339 more interest than Mark's account.

Answer 1

The answer is C) Saul’s account earned $3,338 more interest than Mark’s account

Answer 2

Option D is correct.

Explanation:

Mark deposits $12,000 at the rate of interest 4% for 5 years.

Saul deposits $10,000 at the rate of interest 6% for 8 years.

So first we calculate the maturity amount of both by using the formula :

A = P
`(1+(r)/(n))^(nt)`

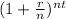
First we calculate Mark's deposit

A = 12,000( 1+0.04/1)
`^(1(5))`

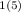
A = 12,000( 1.04)
`^(5)`

A = 12,000 + 2,599.83 = 14,599.83

Mark's maturity amount would be $14,599.83.

Now we calculate the maturity amount of Saul.

A = 10,000 (1+0.06/1)
`^((1)8)`

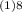
A = 10,000 (1.06)
`^(8)`

A = 10,000 + 5,938.48 = 15,938.48

Saul's maturity amount would be $15,938.48

Therefore to get how much Saul's amount is greater than Mark's account

15,938.48 - 14,599.83 = 1,338.65 rounded to $1,339

Saul's account earned $1339 more interest than Mark's account.